Skip to main content

Selection Sort

In computer science, selection sort is an in-place comparison sorting algorithm. — Wikipedia

Analogy​

Drum Jazz kit

Suppose you have a bunch of songs on your computer.

For each artist, you have a number of plays.

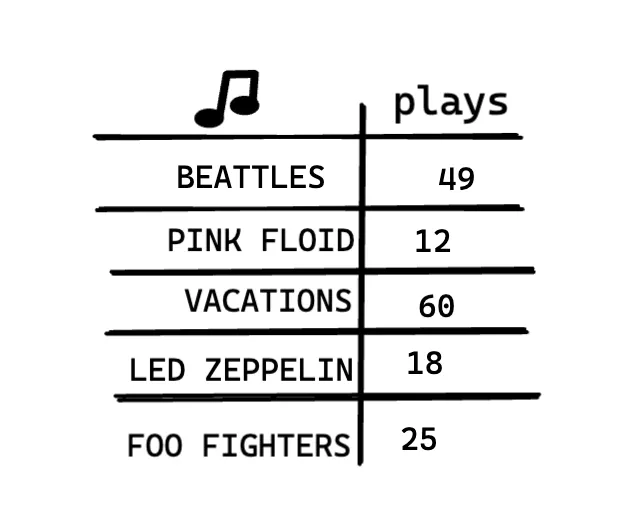
Songs un-sorted

You want to sort this list from most to least played, so that you can rank your favourite artists. How can you do it?

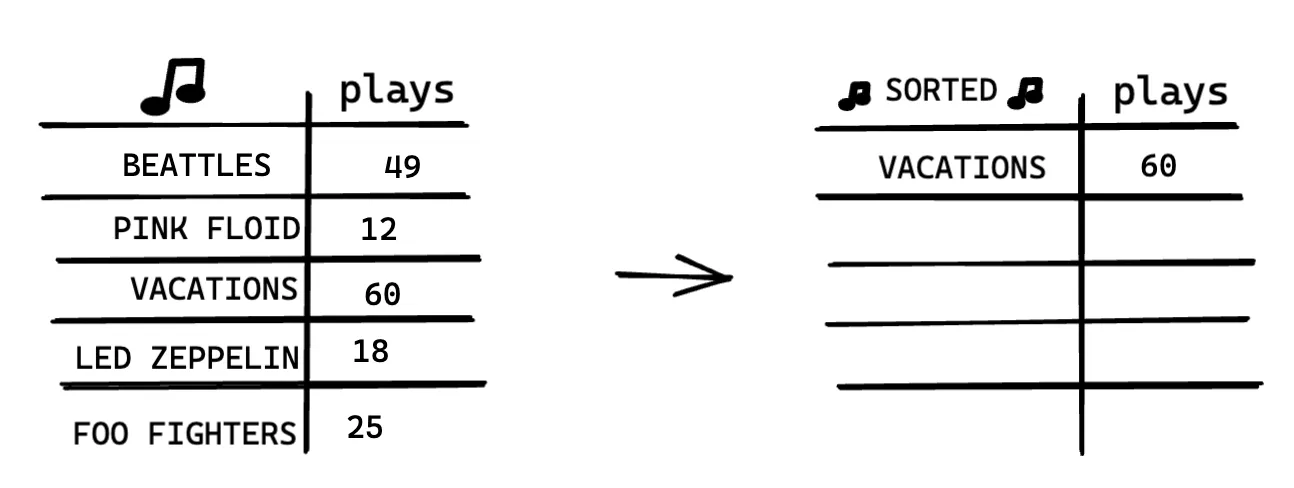
One way is go through the list and find the most played artist. Add that artist to a new list.

Left side: un-sorted list. Right side: sorted list with one song (most played artist).

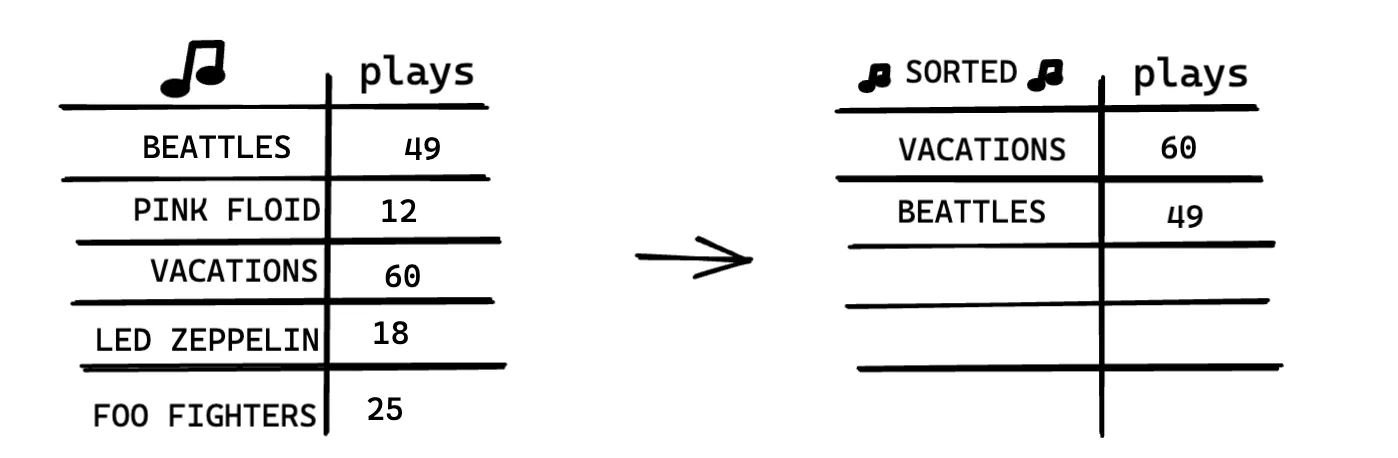
Do it again to find the next most played artist.

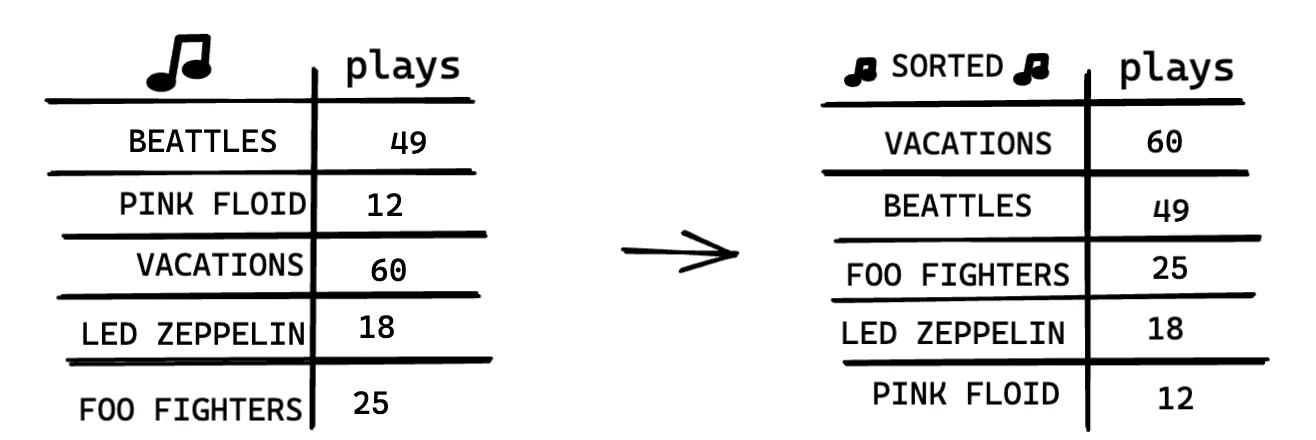
Left side: un-sorted list. Right side: sorted list with two songs (most played artists).

Keep doing this, and you’ll end up with a sorted list.

Left side: un-sorted list. Right side: sorted list.

Time complexity​

To find the artist with the highest number of plays, you have to check each item in the list. This takes O(n) time, as you just saw. So you have an operation that takes O(n) time and you have to do that n times:

This tikes O(n x n) time or O(n^2) time.

Visual representation​

Sort an array from smallest to largest.

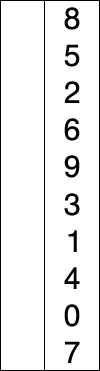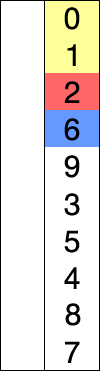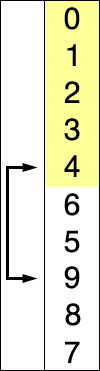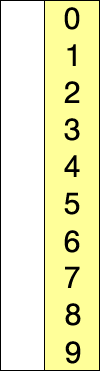
Selection sort animation.

Summary​

Selection sort is the simplest sorting algorithm that works by repeatedly finding the minimum element (considering ascending order) from the unsorted part and putting it at the beginning.

Selection Sort Implementation​

function findSmallest(nums: number[], index: number) {
  let smallest = nums[index];
  let swapIndex = index;
  for (let i = index + 1; i <= nums.length; i++) {
    if (nums[i] < smallest) {
      smallest = nums[i];
      swapIndex = i;
    }
  }
  return { swapIndex, smallest };
}

export default function selectionSort(nums: number[]): number[] {
  for (let i = 0; i < nums.length - 1; i++) {
    const { smallest, swapIndex } = findSmallest(nums, i);
    if (i !== swapIndex) {
      // if smallest is not the current index, swap
      const tmp = nums[i];
      nums[i] = smallest;
      nums[swapIndex] = tmp;
    }
  }
  return nums;
}